머신러닝에서 모델 학습을 시키면 평가지표로써 손실 함수가 등장한다. 손실 함수의 값은 모델이 실제값에 대해서 얼마나 잘 예측했냐를 판가름하는 좋은 지표가 된다. 손실 함수의 값이 작아지면 작아질수록, 모델은 더욱더 예측을 잘하게 된다. 따라서 머신러닝에서 성능을 향상시키기 위해 손실함수를 최소화시키는 방안을 찾게 된다.
손실 함수는 측정 방법에 따라 여러 가지가 존재하게 된다. 사용하는 함수는 각 함수의 특성에 따라 상황에 적절한 함수를 사용한다.
1. MSE (Mean Squared Error)
이름에서 알 수 있듯이 평균제곱오차이다. MSE는 가장 기본적이고 간단한 손실 함수이다. 손실함수의 값은 전체 데이터셋에 대해서 실제값과 예측값의 차이를 제곱한 후 평균을 낸 값이다. 통계학에서의 분산과 비슷한 개념으로 볼 수 있다. MSE의 식은 아래와 같다.

MSE는 제곱한 후에 평균을 내는 방식이기 때문에 이상치가 많이 존재한다면, 과대평가할 가능성이 있다.
2. MAE (Mean Absolute Error)
데이터셋에 이상치가 많아 MSE로 평가하기에 문제가 있을때, MAE를 손실 함수로 사용할 수 있다. MAE는 평균절대오차로, 실제값과 예측값의 차이를 평균하는 방식이다. 에러를 제곱시키지 않기 때문에 MSE에 비해서 이상치에 비교적 강건하다는 장점이 있다. MAE의 식은 아래와 같다.
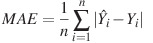
3. RMSE (Root Mean Squared Error)
RMSE는 MSE에서 루트를 씌워준 값이다. 회귀 문제에서 전형적인 평가지표로 자주 사용한다. MSE처럼 이상치가 많이 존재한다면, MAE를 대신 사용하기도 한다. RMSE의 식은 아래와 같다.

분류 문제에서도 평가지표로 손실 함수가 쓰인다. 그러나 분류 문제에서는 예측값과 실제값의 차이를 수치로 나타낼 수 없기 때문에 엔트로피를 대신 사용한다. 엔트로피는 원래 물리학에서 분자의 무질서함을 측정하는 열역학 개념이지만, 여기에 착안해서 정보학에서 엔트로피는 정보의 양으로써 신호를 인식하는 데에 쓰인다. 정보 이론에서 사건 발생 확률이 낮다는 것은 곧 많은 정보를 가지고 있다는 뜻이고, 엔트로피가 높아진다는 이야기이다. 엔트로피 식은 아래와 같다.

엔트로피는 확률 * log(확률)의 합이다. 예를 들어 이진 분류 문제에서 네 개의 데이터에 대해 레이블이 1일 확률이 [0.4, 0.9, 0.6, 0.1]이 나오고 실제 레이블이 [0, 1, 1, 0] 이라면 엔트로피는
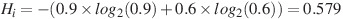
가 된다.
1. Cross-entropy
Cross-entropy는 위의 정보 이론의 엔트로피 개념에서 착안되었다. Cross-entropy란 실제 분포를 모를 때, 모델링을 통해서 실제 분포를 예측하고자 하는 것이다. 예측 모델 p와 실제 모델 q에 대한 Cross-entropy의 식은 다음과 같다.
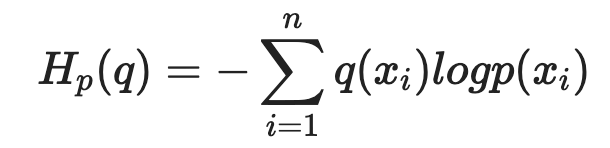
이 때, 이 계산은 이산확률분포를 전제로 한다.
분류 문제에서 Cross-entropy가 사용될 수 있는 이유는 분류기의 결과값이 각 클래스에 속할 확률로써 나타내어질 수 있기 때문이다.
예를 들어보자.
실제 클래스에 대한 분포를 P라고 하고, 예측 클래스에 대한 분포를 Q라고 하자. 그리고 다음과 같이 실제 레이블과 확률이 주어졌다고 가정하자.
p = [1, 1, 1, 1, 1, 0, 0, 0, 0, 0]
q = [0.8, 0.9, 0.9, 0.6, 0.8, 0.1, 0.4, 0.2, 0.1, 0.3]그러면, Cross-entropy는 다음과 같이 계산된다.
[y=1.0, yhat=0.8] ce: 0.223
[y=1.0, yhat=0.9] ce: 0.105
[y=1.0, yhat=0.9] ce: 0.105
[y=1.0, yhat=0.6] ce: 0.511
[y=1.0, yhat=0.8] ce: 0.223
[y=0.0, yhat=0.1] ce: 0.105
[y=0.0, yhat=0.4] ce: 0.511
[y=0.0, yhat=0.2] ce: 0.223
[y=0.0, yhat=0.1] ce: 0.105
[y=0.0, yhat=0.3] ce: 0.357
Average Cross Entropy: 0.247분류 문제에서는 분류 클래스의 개수에 따라 Cross-entropy를 구하는 방식이 달라지게 된다.
2. Binary Cross-entropy
Binary cross-entropy는 0과 1의 레이블만 갖는 이진 분류 문제에서 사용된다. 식은 다음과 같다.

3. Categorical Cross-entropy
Categorical cross-entropy는 MNIST데이터셋과 같은 다중 클래스 분류 문제에서 사용된다. 식은 다음과 같다. 소프트맥스 함수를 사용하기 때문에 소프트맥스 손실이라고도 불린다.
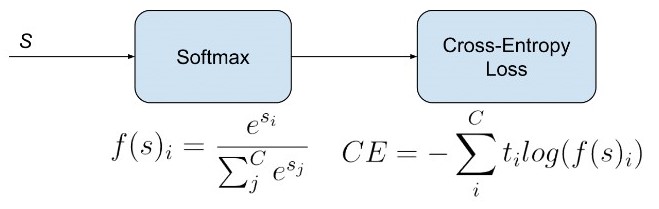
4. Sparse Categorical Cross-entropy
Sparse categorical cross-entropy는 categorical cross-entropy와 마찬가지로 다중 클래스 분류 문제에서 사용된다. Categorical cross-entropy와 다른 점은 Sparse는 클래스들이 0,1,2 등과 같은 정수일 때 사용한다는 점이다.
참고자료
[1] "Introduction to Loss Functions", DataRobot, 2018, https://www.datarobot.com/blog/introduction-to-loss-functions/
[2] Jason Brownlee, "A Gentle Introduction to Cross-Entropy for Machine Learning", Machine Learning Mastery, 2019, https://machinelearningmastery.com/cross-entropy-for-machine-learning/
'Data Science > Machine Learning' 카테고리의 다른 글
| [Machine Learning] 데이터 전처리(1) - 결측치 처리(1) (0) | 2023.06.22 |
|---|---|
| [Machine Learning] 평가 지표 - 분류(Classification) (0) | 2023.02.07 |
| [Machine Learning] 분류 알고리즘 (0) | 2023.01.29 |
| [Machine Learning] 지도 학습 vs 비지도 학습 vs 강화 학습 (0) | 2023.01.19 |
| [Machine Learning] scikit-learn에 대하여 (0) | 2023.01.18 |



